Embedding mathematical expressions
Problem
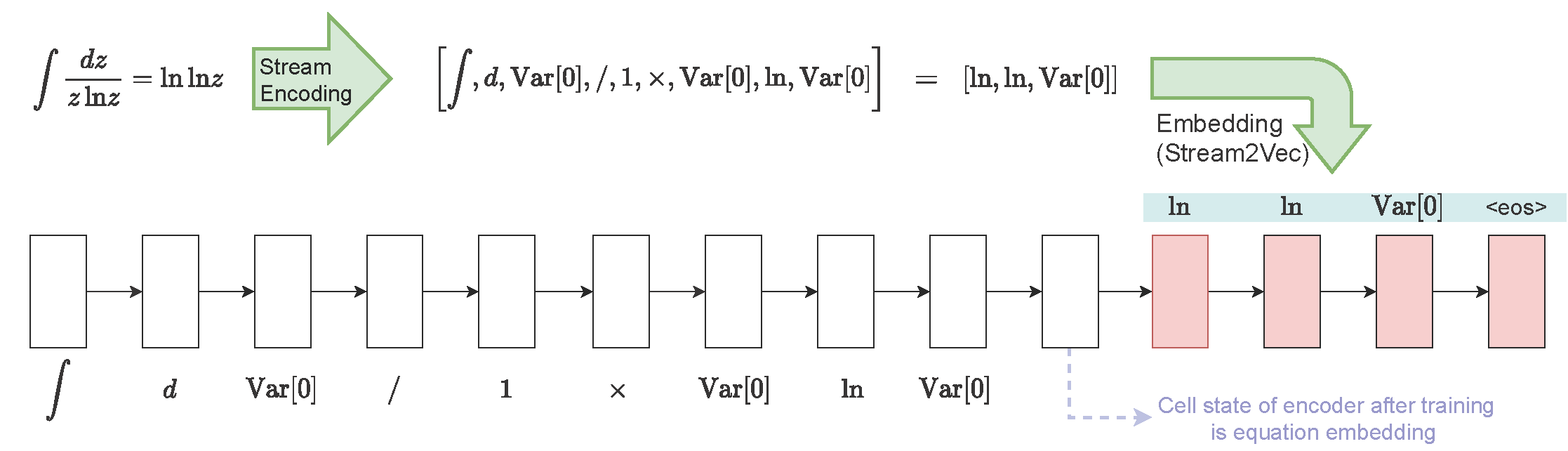
Embedding mathematical data is a significant challenge that has attracted some significant attention in recent years. While in natural languages, one has a finite set of words ordered along a single dimension, mathematical equations are significantly more complex. Consider the equation $z^3 = \frac{x}{y} - 6$. Visually, the individual symbols are arranged along two dimensions and semantically the equation displays a tree like structure. This is in contrast to natural languages where words are arranged along a single dimension.
However, the extra-dimensional layout complexity isn’t the only problem. The mathematical equation can be written in a multitude of semantically-equivalent forms; e.g., using differing symbol layouts ($\frac{x}{y}$ vs. $x/y$ vs. $x \cdot y^{-1}$), additional or differing constant values ($\sin(2x)$ vs. $\sin(x)$) and approximately equivalent operators (\(\sin(x)\) vs. $\cos(x-\frac{\pi}{2})$). These effects do not alter the semantic meaning of an expression despite significantly altering its visual presence. Hence, there is a need to device embedding schemes that capture equation semantics while being minimally impacted by symbolic layout. \textit{Effective language processing methods must be able to ignore trivial visual variations and embed mathematical content according to semantic meaning. }
Our Approach
In natural-language embedding, textual-sequence encoding is accomplished using the assumption that sentences close in proximity have similar meanings. With mathematical expressions, we argue two expressions are similar if they are semantically-equivalent according to the rules of mathematics. Building upon modern methods of embedding, we propose embedding a mathematical expression according into an n-dimensional vector without the aide of textual descriptors using modified sequence-to-sequence neural networks . As shown in the figure above, we can use NLP embedding techniques trained on a corpus of semantically-equivalent mathematical expressions to obtain a semantic-based formula embedding model.


